Epistemic status: pretty uncertain. There is a lot of fairly unreliable data in the literature and I make some pretty crude assumptions. Nevertheless, I would be surprised though if my conclusions are more than 1-2 OOMs off though.
The brain is currently our sole example of an AGI. Even small animals with tiny brains often exhibit impressive degrees of general intelligence including flexibility and agentic behaviour in a complex and uncertain world. If we want to understand how close contemporary machine learning is to AGI it is worth getting a quantitative sennse of the brain. Although a lot of excellent work has been done on analyzing the capacity of the brain and what it means for AI timelines, I never feel as if I have really understood something until I’ve done it myself. So, here is my analysis of the brain in terms of modern machine learning, and what it may suggest about AGI development.
The first step, which is what is done here, is to try to get a rough quantitative grasp on the numbers in play for the human brain compared to current ML systems. First, we need to understand how many neurons and synapses are in the brain so we can compare to large scale ML systems. For number of neurons, general estimates range from between 80-100B neurons for the human brain. An important point, which is often not emphasized in comparisons of the brain to ML, is that the brain is not a single monolithic system but is composed of many functionally specialized and architecturally distinct subunits. To begin to really understand what is going on, we need to know how these 80-100B neurons are distributed between different brain regions.
It turns out to be exceptionally hard to find concrete and reliable numbers for this 1 . The best and closest data I could find which is comprehensive is from the blue brain atlas for the mouse. Here is the fraction of neurons plotted for each macroscale region of the mouse brain (the total number of neurons in a mouse is about 100M).
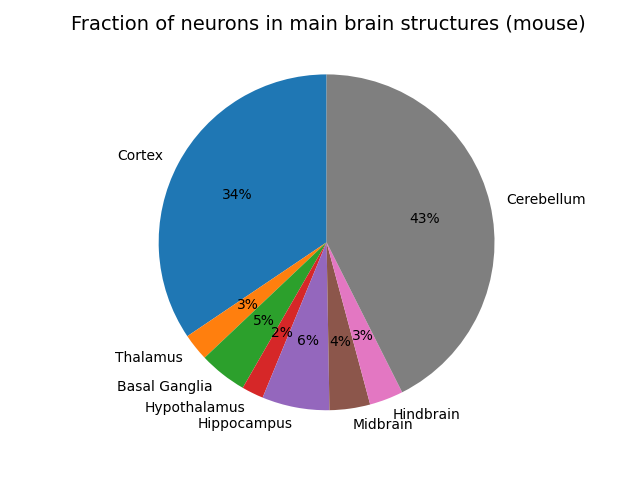
There are a couple of big surprises for me which probably shouldn’t have been. The first is how huge the cerebellum is. It has more neurons than the whole cortex! The fact that we still have relatively little idea what the cerebellum does or how it works despite its huge size and extremely regular structure is probably a huge oversight in neuroscience. Secondly, the hypothalamus and thalamus are both much larger than I imagined them as being, probably because they are often described in terms of nuclei, which are usually assumed to be small. The hippocampus and basal ganglia also take up good fractions of the total count, comparable in size to a large cortical modality like audition which takes up an appreciable fraction of cortex. The hindbrain (medulla and pons) and midbrain (tectum and tegmentum) are actually less volume than I would have thought, considering these alongside the hypothalamus form the evolutionary most basic brain regions, and can sustain basic behaviour alone. In humans, I expect these broad proportions at approximately the same fractions as in the mouse since it appears that the cortex to cerebellum ratio seems constant across species. The cortex/cerebellum probably takes up a slightly larger fraction of the total compared to the rest in humans than in mice however.
The cortex itself is not uniform but specialized into different regions which perform different functions. The blue brain atlas also provides a breakdown of the proportion of these areas in mice,
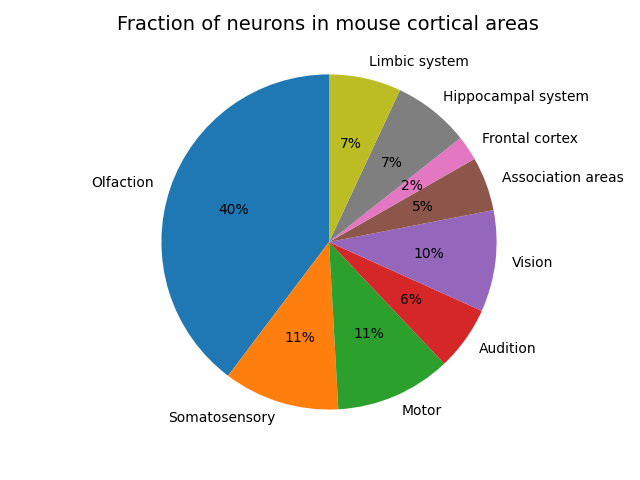
I expect these proportions to differ quite a bit compared to the human. Especially in sensory processing areas. The mouse dedicates an incredible amount of its cortical real-estate to olfaction, and not much to vision and audition. I don’t have super great data for humans but from what I can see it’s approximately the other way around with 27% or cortical real-estate dedicated to vision, a similar amount (8%) to audition and much less (probably around 2-3% to olfaction). I expect that the humans will have larger association areas and also a larger frontal region. For neuroscientists, by ‘association areas’ I’m talking about the posterior parietal and temporal lobe regions involved in producing high level abstract multimodal stimulus representations. Similarly, for the ‘hippocampal system’, I’m talking about the perirhinal, entorhinal and retrosplenial cortex which is involved in maintaining episodic memory and spatial maps of the environment, and for the ‘limbic system’, I mean the anterior cingulate and insula cortices. This proportion might be smaller than humans as mice and rats appear to maintain a larger than average retrosplenial cortex involved in navigation than humans do. Overall though, we cannot just directly cmopare the number of neurons in the cortex or indeed the whole brain to ML models until our ML models are actually performing all the tasks that animals can.
Let’s now figure out how to scale these mice figures up for humans. According to this source (which seems pretty reliable), humans have about 86B neurons compared to a mouse’s 70-100M neurons, so a human brain has approximately 1000x the neurons of a mouse. Also according to the paper, of the 86B neurons, only 16B are in the cerebrum and 70B are in the cerebellum (!), so the cerebellum absolutely dominates the total neuron count. Of course neurons are not necessarily what matters in that effective parameters come primarily from synapses. Looking at estimates, we have approximately 1000-10000 synapses per cortical pyramidal neuron. Let’s take this as the base but use the low side of the estimate since not all neurons are pyramidal (many interneurons) and these probably have fewer synapses. Subcortical regions, which are included in the neuron count also probably have lower average synapse count, but consistent data is hard to find on this also. 1000 synapses/neuron is also a very easy number to work with and we only really care about OOMs for our analysis. If we take these numbers seriously, then we can expect the whole cortex to contain about 16B neurons and hence 16T parameters, about 2 OOMs larger than large language models like GPT3.
Of course our entire brain isn’t doing language modelling, only a relatively tiny proportion of it is. Specifically, we know that in humans we have specialized regions involved in language comprehension and understanding: Broca’s area and Wernicke’s area. These comprise relatively small amounts of the brain. Again, information about the exact volumes taken up by these areas is hard to find, but together they take up 3 Brodmann areas out of approximately 50 so this means approximately 6% of the cortical volume is made up of language focused areas which, to me, seems like a sensible estimate, if a little high. Effectively, this says that we dedicate an amount of cortical real estate to language comparable with a significant sensory modality like olfaction or somatosensory perception but not as much as a fundamental modality like vision or hearing.
If we assume that our language modelling capabilities are located primarily in Broca’s and Wernicke’s areas then we get an estimate of approximately 400-700M neurons and hence 400-700B paramaters devoted to language modelling in the brain. Interestingly, this is at rough parity with or just slightly greater than the current state of the art (PaLM is approximately 540B, Gopher is 280B). If we assume a naive approximately equal scaling between parameters in the brain and transformer parameters then this would imply that current language models are approximately at human levels of performance. I would argue this is actually pretty accurate to within an OOM or so – language models are much better than people at some tasks, much worse than others (which usually involve abstract logic, long term consistency etc which likely depend on other brain regions and/or physical symbol grounding), but on the other hand Broca’s and Wernicke’s areas probably do other functions than pure language modelling (such as motor control for speech production) which means they don’t get to use their full parameter count. This result is actually quite surprising to me, since it seems to imply that the brain and current ML methods have a roughly equivalent scaling law for parameter count (data is another story) 2.
If we naively assume that this rough parameter equivalence (to within an OOM) of ML and the brain might apply to our other senses and cognitive abilities. Let’s first look at vision. Unlike Broca’s area which is relatively small, the visual cortex as a whole is massive. Again, it’s hard to find precise numbers, but I’ve seen a rough estimate at about 30% of our cortical volume is dedicated to vision, which seems about right to me (definitely within 15-40%). At that level, then approximately 3-5B neurons and 3-5T synapses would be involved in vision so we should expect ‘human competitive’ vision models to start appearing about an OOM above the current scale of our language models. However, current SOTA vision models are significantly smaller than our langauge models at present. SOTA imagenet models are of order 100M parameters, stable diffusion sits at about 900M, and Dalle-2 has 12B parameters (although the majority of that is the natural langauge component, I think). This means that from where we are currently it would take about 3-4 more OOMs of scaling to reach human competitive vision.
However, current visual recognition and image generation is already really good, and seems closer to parity with humans than 3-4 OOMs. One possibility is that current ML vision architectures are intrinsically more efficient than the brain. Perhaps weight sharing with CNNs or parallel sequence prediction with transformers and similar architectural innovations that the brain can’t match are central to this. Alternatively, the brain has to solve a much harder problem which is essentially flexible video generation and interpretation, and that perhaps it will take us several more OOMs of parameter count to fully crack video. That also wouldn’t surprise me as our current video capabilities seem pretty lacking. We really need scaling laws for visual models to get to the heart of this question.
A similar result applies to audio. The auditory cortex takes up about 7% of the cortex. This boils down to approximately 700M-1B neurons and hence 700B-1T parameters for a human competitive auditory system. OpenAI’s whisper model, by contrast, appears to achieve near-human parity in speech-to-text with only 1.2B parameters, again implying that either the brain is very inefficient at audio, or that the brain has much greater audio capabilities than current ML models.
What about the rest of the brain? This analysis is pretty straightforward to do given the proportions of cortex above. The estimate for number of synapses per neuron are probably different in subcortical regions like the hippocampus and basal ganglia are probably lower, so their parameter count should get adjusted lower accordingly. This still means though, that the brain has vast (100B-1T) models dedicated to doing things like model-free RL (basal ganglia) and memory-consolidation and spatial navigation (hippocampus).
A similar argument applies to the cerebellum where although it has a vast number of neurons, these are almost entirely cerebellar granule cells which make only a reasonable small number (approx 5) of synapses. There are also a much smaller number of about 15M purkinje cells which each have between 10-100 thousand synapses each. Taken together, this gives the cerebllum an effective parameter count of about 500B-1T, or about the size of a large cortical region but not completely dominant. Funnily enough, this sounds about right for the functional impact of cerebellar operations.
How big of a network, then, do we need to build a full brain? Given approximately 20B non-cerebellar neurons and if we assume that the cerebellum has an effective parameter count of about 1T, then my estimate that the effective parameter count of the full brain is somewhere between 10-30T parameters. This is extremely large but within only 1-2 OOMs of current large scale systems. Based on estimates of the cost of training GPT3 and its parameter count, if we assume a linear cost per parameter then this works out to be within 100M-1B to train an NN equivalent to the brain today.
So what does the brain look like to a machine learner? It looks like a set of about 10-15 semi-independent specialized models, each ranging from about the size of PaLM up to maybe an OOM larger, which are each independently specialized in and control some specific modality or function. These models also have extremely high bandwidth interconnect with eachother and communicate intensively throughout both inference and learning phases. These large-scale models, which comprise the ‘learning from scratch’ part of the brain are also surrounded by a thin layer of more hardcoded functionality which is tiny in number of parameters but highly influential in practice. This hardcoded functionality handles collecting and preprocessing of inputs, postprocessing of outputs (especially motor), dynamically setting objectives like the reward function in accordance with the current homeostatic state, and performing global modulation of things like your attention, alertness, arousal levels etc in response to external stimuli. These models all operate in real time, with a latency of about 100-200ms for a full run through of perception, planning, action selection, and then motor implementation. They are trained on a relatively small (but not tiny) amount of non-i.i.d data, in an online POMDP environment and with a minibatch size of 1.
If we look at this in comparison to modern machine learning, while such systems are far beyond current capabilities, if progress and investment in ML continues at the same rate we have observed over the last decade, then it is highly plausible that we can scale up a few more OOMs in the next decade. There are probably some additional architectural details to work out, and we likely need more data efficient architectures or training methods, but there doesn’t appear to be any fundamental blockers in the way. Hence why I have pretty short timelines.
The data question
A fundamental question that arises in these analyses relates to the scaling of data while we have only considered parameters. The Chinchilla scaling laws again bring data back to the forefront and make it clear that this will be the primary constraint on scaling for large language models from now on. In the context this is even more important since the brain does not get trained on the entire internet. In fact, we can quite easily set an upper bound on this. Imagine you read constantly your entire life (for 80 years) at 250 words per minute for 80 years. This is only approximately 10B tokens, an order of magnitude less than even the insufficient data current language models are trained on. A similar situation prevails with images. For the upper bound, let’s assume we perceive at 60 FPS for our entire life of 80 years. This is only 2.5B images – a large number but much less than the entire video content of youtube. These numbers are pretty high upper bounds and are already too small by large scale machine learning standards and the chinchilla scaling laws (although to be fair we don’t yet have any equivalent scaling laws for image/video data and it may be that these are much more data efficient than language, although that seems unlikely).
There are two options here that form a spectrum. a.) Data is fundamentally the constraint on intelligence in humans and that due to lack of data the brain is forced to have a huge number of parameters to keep scaling, so is far off the optimal scaling curve. b.) the brain is much more data efficient and hence operates on a different scaling law where data is much less important. Personally, I think option b is more likely with some shades of a (the brain having too many parameters) is also possible. I have a couple of arguments for this but in my opinion they are not definitive.
1.) Humans (and animals) probably get better data than AI systems. Humans can go out and interact with the world and seek out desired rather than being fed i.i.d random and redundant data from the internet. This probably puts them on a better scaling law, especially with Zipfian distributed data where rare tokens/data could be incredibly unlikely to appear under purely random sampling. Effectively, through action, humans get to importance sample their data.
2.) If data is truly the bottleneck, then evolution would put enormous pressure on optimizing the data efficiency of the architecture. This hasn’t yet happened in ML as up until now we have primarily had compute be the bottleneck for state of the art results. It seems unlikely a priori that current architectures are optimally data efficient.
3.) Different animals i.e. us vs small monkeys and maybe even mice or small mammals probably get roughly similar amounts of visual and auditory data input, yet evolution keeps scaling up our visual and auditory cortices. This seems unlikely if we are on a extremely bad scaling law with respect to these modalities. Interestingly, this may have been the case with olfaction where we typically see the olfactory cortex shrink in relative size with larger brains.
4.) We know that on lots of tasks that humans tend to be (but are not always) more sample efficient than current ML models, which may imply they are more sample efficient in general and hence have a better parameter-data scaling law.
Assumptions in the model
The model here is extremely simple and only intended to be accurate up to (hopefully) 1 OOM but maybe 2. I would be surprised if the numbers were more off than that even given all the simplifying assumptions.
1.) Synapses are not identical to NN parameters. There are two arguments here. First that synapses are lower precision than 32bit floats which are the usual way to represent NN weights. Synapses are noisy and probably can carry only a relatively small number of bits of information, which would lower the ‘effective parameter count’ of a synapse. On the other hand, synapses also have capabilities ANN weights do not, like having both fast and slow weight learning and hence implicitly implementing some kind of fast-weight scheme.
2.) Neurons in the brain are more complex than ANN neurons. This is true but I think the effect is minor compared to the number of synapses. Neurons can definitely do things like adjust their threshold to inputs, and be modulated in various ways by various neurotransmittors. However, suppose this means that each neuron has 5 additional learnable parameters. This is tiny in comparison to the 1000-10000 parameters encoded in its synapses. On the other hand, these parameters means that brains are much better able to adapt processing ‘on the fly’ during inference than ANNs which compute a fixed function. This is plausibly very useful for dynamically modulating behaviour on a short timescale but likely has little influence on the longer timescale of weight learning.
3.) The dendritic tree is more complex than a linear sum of all synaptic inputs – i.e. synapses which are closer to the soma get weighted more. There are multiple dendritic integration zones (basal, apical etc). Perhaps dendrites can multiplicatively interact with eachother i.e. some synapses can gate other synapses or something. This is all possible and I don’t have a good model of how this increases the effective parameter count of a neuron.
4.) The brain may use a learning algorithm that is more/less efficient than backprop. The brain probably doesn’t use backprop for credit assignment due to issues with locality and parallelizability but must learn in some other way. Backprop is already very efficient so a priori it is likely that this algorithm is worse. On the other hand, the general cortical credit assignment algorithm would be under intense selective pressure by evolution so it is probably pretty good and maybe even better than backprop. I believe there are better algorithms out there (but then I would). Since we currently have very little idea how credit assignment is done in the brain, then this is a huge open question and source of uncertainty in the brain’s effective parameter count.
Biological scaling laws
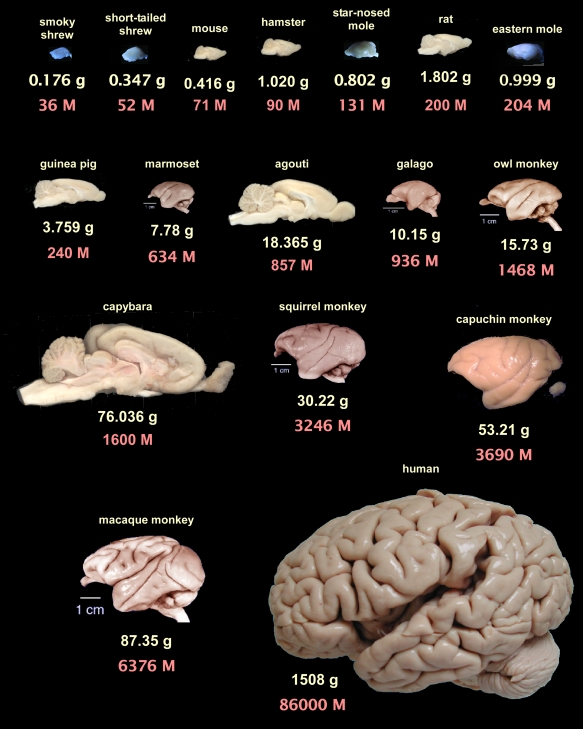
With all the focus on scaling laws in machine learning, it is worth looking at what we have discovered about scaling laws in neuroscience. It is now clear that our conception of the ‘intelligence’ of a species is closely correlated to the number of neurons that they possess, implying a relatively smooth parameter-performance scaling law also exists in nature. Without some kind of objective intelligence measure across species, we can’t estimate the exact scaling coefficients like in machine learning, but it is clear that such a law exists. There is no reason to believe that it would stop working immediately at human level.
Fascinatingly, according to this paper, there are actually multiple biological scaling laws relating brain size to neuron count. Most mammals are on a relatively bad scaling law where, as the neuron count increases, the number of supporting glial cells must increase by a greater proportion, and the size of neurons must also increase. This means that increasing proportions of the brain must be devoted to glial cells and neuronal density falls so they run into sharply diminishing returns on scaling. Primates, in contrast, appear to have found a significantly better scaling law which allows us to scale neurons and glial cells 1:1 and to keep neural density constant across scales. This allows us to support vastly more neurons for a given large scale brain and explains why we are significantly more intelligent than larger animals like whales or elephants which have substianlly larger brains than us.
The human brain itself appearsto fit exactly within the bounds predicted by the primate scaling laws for its size 3. Without some cross-species measure of objective intelligence, it is hard to tell whether humans are smarter or less smart than would be predicted by a scaling of primates. The ‘standardness’ of the human brain to me also implies that there is no reason we should expect scaling to fail beyond this point. If we were to build/evolve much larger brained primates, we would expect them to be smarter than us.
The size of the human brain appears to be limited primarily by the caloric requirements of its upkeep, where it costs about 25% of our total energy budget. Additional constraints on our brain size may include cooling requirements as well as having small enough heads to be able to be born. However, a brain energy budget of 25% does imply that there is a meaningful trade-off against body-size and capability and that ‘more intelligence’ is not always hugely valuable, at least in the ancestral environment. I.e. there appears to be no physical reason why a brain energy budget of 50% would be impossible if intelligence were extremely marginally valuable up to those levels, so out current 25% budget implies that each marginal unit of intelligence we get above this point is equally valuable as a unit of energy invested in better muscles or internal organs or whatever. To me this implies that we should expect additional scaling of the brain to probably show diminishing returns, as in the standard power law scaling we get from ML. This, of course, applies primarily to the ancestral environment and not our current environment.
It is worth thinking about whether a similar argument would apply to ML scaling also. All evidence we have now is that scaling is strongly sublinear (power-law) returns and thus each marginal gain in ‘intelligence’ is obtained at an ever greater cost. This is very different to the superlinear scaling required for a FOOM scenario where intelligence helps to increase further intelligence gains. In a future post I’ll write more about this and what it means for models of AGI .
-
It is really surprising how bad neuroscience is about collecting and making available reliable data for even the most basic global questions like this. ↩
-
Data is especially important in light of the new Chinchilla scaling laws where they show that a data-optimal training schedule enables greater performance than Gopher and PaLM with just an 80B parameter model but trillions of datapoints. If, somehow, we assume that the brain operates on a Chinchilla-like instead of GPT3-like scaling curve, then again we should expect the brain’s language modelling to be about 1 OOM above the current state of the art (i.e. however good a 700B Chinchilla would be) ↩
-
In general, I am extremely confused by the magnitude of the effect of individual differences in intelligence (IQ) on performance for what must be relatively minor differences in the brain given a.) the extremely slow power-law scaling implied by ML scaling laws and b.) a similarly slow scaling law existing between species. I will write a follow up post on this shortly. ↩